Orthogonales Sudoku/de: Unterschied zwischen den Versionen
Aus Puzzlewiki
Zur Navigation springenZur Suche springen
Berni (Diskussion | Beiträge) Die Seite wurde neu angelegt: „{{TAXOBOX | Ordnung = Füllrätsel | Familie = Vollgitterfüllrätsel | Gattung = Lateinische Quadrate | Art = Orthogonales Sudoku }} ==Anleitung== {{BE…“ |
Berni (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
==Anleitung== | ==Anleitung== | ||
{{BEISPIEL| | {{BEISPIEL|orthogonales_sudoku}} | ||
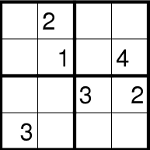
''Tragen Sie die Zahlen 11, 12, ..., 44 so in das Diagramm ein, dass jede Zahl in genau einem Gebiet vorkommt und sowohl die vorderen Ziffern, als auch die hinteren Ziffern ein korrektes Sudoku ergeben.'' | ''Tragen Sie die Zahlen 11, 12, ..., 44 so in das Diagramm ein, dass jede Zahl in genau einem Gebiet vorkommt und sowohl die vorderen Ziffern, als auch die hinteren Ziffern ein korrektes Sudoku ergeben.'' | ||
| Zeile 18: | Zeile 18: | ||
* [http://www.logic-masters.de/Raetselportal/Raetsel/zeigen.php?id=000010 Rätselportal: Orthogonales Sudoku] | * [http://www.logic-masters.de/Raetselportal/Raetsel/zeigen.php?id=000010 Rätselportal: Orthogonales Sudoku] | ||
* [http://www.logic-masters.de/Raetselportal/Raetsel/zeigen.php?id=000012 Rätselportal: Orthogonales Sudoku] | * [http://www.logic-masters.de/Raetselportal/Raetsel/zeigen.php?id=000012 Rätselportal: Orthogonales Sudoku] | ||
* [http://www.logic-masters.de/Raetselportal/Raetsel/zeigen.php?id=00002K Rätselportal: Orthogonales Sudoku 3] | |||
[[Kategorie:Haupträtselart/de]] | [[Kategorie:Haupträtselart/de]] | ||
<!-- In Meisterschaften --> | <!-- In Meisterschaften --> | ||
Aktuelle Version vom 25. Februar 2018, 20:12 Uhr
| Systematik | |
|---|---|
| Ordnung: | Füllrätsel |
| Familie: | Vollgitterfüllrätsel |
| Gattung: | Lateinische Quadrate |
| Art: | Orthogonales Sudoku |
Anleitung
Tragen Sie die Zahlen 11, 12, ..., 44 so in das Diagramm ein, dass jede Zahl in genau einem Gebiet vorkommt und sowohl die vorderen Ziffern, als auch die hinteren Ziffern ein korrektes Sudoku ergeben.
Weblinks
- Rätselportal: Orthogonales Sudoku
- Rätselportal: Orthogonales Sudoku
- Rätselportal: Orthogonales Sudoku 3