Binärer Rundweg/de: Unterschied zwischen den Versionen
Aus Puzzlewiki
Zur Navigation springenZur Suche springen
Berni (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Berni (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (5 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{TAXOBOX | |||
| Ordnung = Streckenzugrätsel | |||
| Familie = Verzweigte Streckenzugrätsel | |||
| Gattung = Verzweigte Streckenzugrätsel mit Sackgassen | |||
| Art = Binärer Rundweg | |||
}} | |||
==Anleitung== | ==Anleitung== | ||
{{BEISPIEL|binaerer_rundweg}} | |||
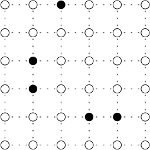
''Zeichnen Sie auf den Gitterlinien einen Rundweg aus sich nicht überlappenden Linien der Länge 2, der durch alle schwarzen Punkte geht. An weißen Punkten kann, an schwarzen Punkten muss der Weg eine T-Form haben. Jede Linie berührt genau zwei andere Linien. Der Weg benutzt alle Linien. Es dürfen keine geraden Linien mit einer Länge größer 2 entstehen. | ''Zeichnen Sie auf den Gitterlinien einen Rundweg aus sich nicht überlappenden Linien der Länge 2, der durch alle schwarzen Punkte geht. An weißen Punkten kann, an schwarzen Punkten muss der Weg eine T-Form haben. Jede Linie berührt genau zwei andere Linien. Der Weg benutzt alle Linien. Es dürfen keine geraden Linien mit einer Länge größer 2 entstehen. | ||
| Zeile 7: | Zeile 14: | ||
<div style="clear:both"> </div> | <div style="clear:both"> </div> | ||
== | == Links == | ||
* http://inabapuzzle.com/honkaku/bloop.html | * http://inabapuzzle.com/honkaku/bloop.html | ||
[[Kategorie:Haupträtselart/de]] | [[Kategorie:Haupträtselart/de]] | ||
<!-- In Meisterschaften --> | <!-- In Meisterschaften --> | ||
[[en:Binary Loop]] | [[en:Binary Loop]] | ||
Aktuelle Version vom 8. Juni 2014, 10:09 Uhr
| Systematik | |
|---|---|
| Ordnung: | Streckenzugrätsel |
| Familie: | Verzweigte Streckenzugrätsel |
| Gattung: | Verzweigte Streckenzugrätsel mit Sackgassen |
| Art: | Binärer Rundweg |
Anleitung
Zeichnen Sie auf den Gitterlinien einen Rundweg aus sich nicht überlappenden Linien der Länge 2, der durch alle schwarzen Punkte geht. An weißen Punkten kann, an schwarzen Punkten muss der Weg eine T-Form haben. Jede Linie berührt genau zwei andere Linien. Der Weg benutzt alle Linien. Es dürfen keine geraden Linien mit einer Länge größer 2 entstehen.